This blog is part one of a three-part series. Please find part two here and part three here.

Introduction

Most of us are aware of the ground loop in the 2-port measurement. Most of us are also aware that we need to introduce a ground loop isolator to correct the error. If not, we’ve published plenty on the subject. But how much CMRR do you need to add? How does the use of a probe impact this requirement?  

Rest assured, this measurement can be successfully performed, as shown in Figure 1, and we’ll show you how to determine much CMRR it takes in this blog.

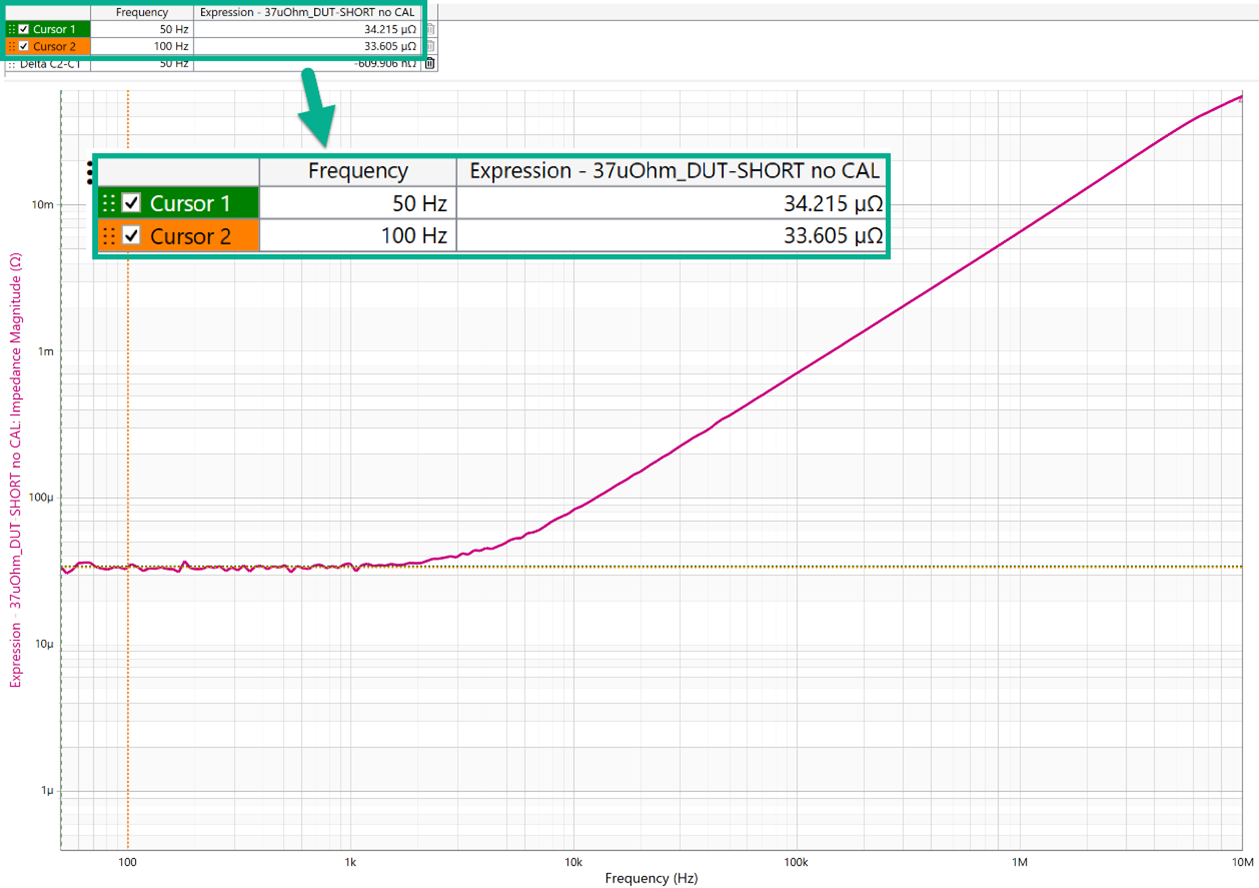Figure 1. Depiction of 37 µΩ Known DUT 2-port shunt through impedance measurement.

Companies like Intel, Nvidia, AMD, Qualcomm, and Broadcom are putting more cores on a single die. Ampere is an excellent example where they have designed a cloud processor solution with 192 cores on a single die. While 2000 Amps may seem excessive, the power demands of data centers, supercomputing, and AI have already surpassed this number. Without adding other considerations on the thermal design or PDN validation, let’s focus on what is required to measure a 2000 Amp PDN.

Measuring a 2000 Amp PDN with a 2-port probe or even with two 1-port probes is not intuitive or even trivial. To effectively measure a 2000 Amp PDN, it is important first to understand the desired impedance to be measured to support 2000 Amps. With reference to Equation 1, if it is assumed that a 0.8 V power domain has an 80 mV peak-to-peak ripple spec, then with a 2000 Amp step load, the target impedance (Z_TGT) is 40 µΩ.

The Ground Loop Error

With the understanding of the ZTGT, efforts can be made to understand the requirements to be able to make a measurement a the desired Z_TGT of 40 µΩ. It quickly becomes clear that the common mode rejection ratio (CMRR) becomes an important figure of merit to mitigate the ground loop for successful low impedance measurements into the micro-ohms associated with the two-port shunt through measurement. This method is well-published, so this discussion will not include details.

Figure 1 depicts a 2-port measurement setup using 1-meter PDN cables for a 40 µΩ Device Under Test (DUT). The ground loop error is clearly seen, and the error from this is shown in Figure 2.  

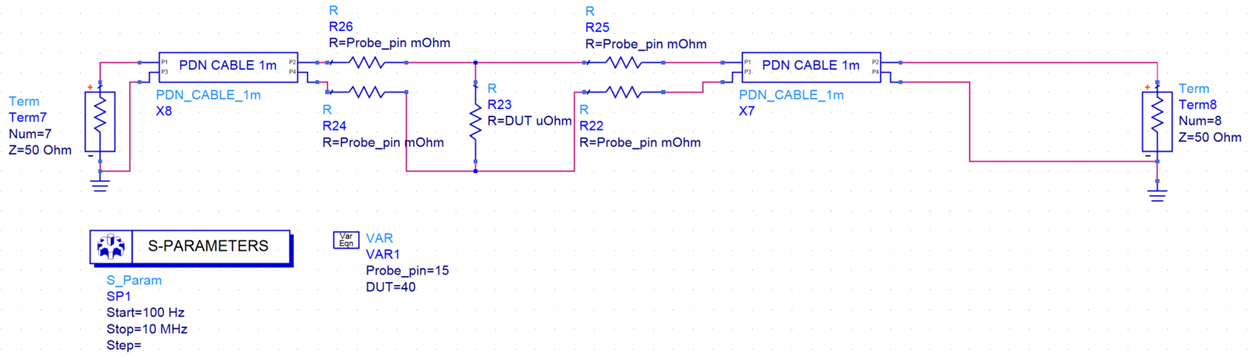Figure 2. 40 µΩ DUT impedance measurement setup with 1-meter PDN cables.

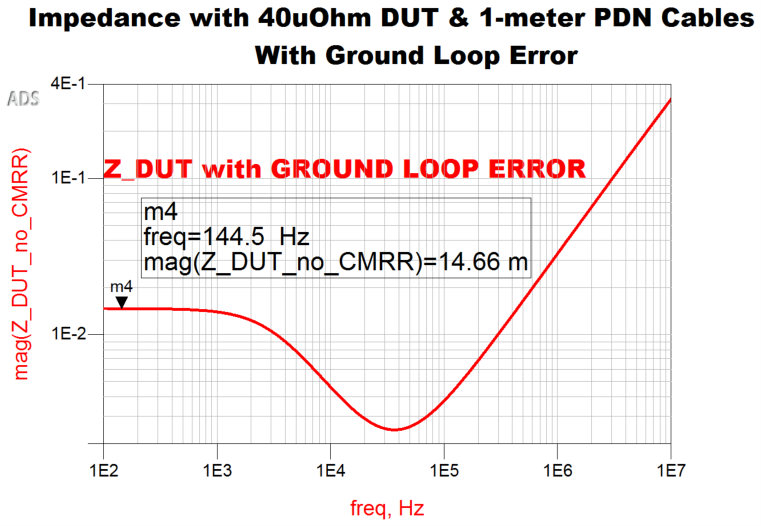Figure 3. 40 µΩ DUT impedance measurement setup with 1-meter PDN cables.

The ground loop resistance is the parallel equivalent of the two cables connecting the VNA to the DUT. In this case, the two cables are identical as are the probe ground pins.  So, the resistance of a single cable and probe pin is twice this measured value.

The return resistance is the sum of the cable shield and pin resistance.  

By substitution

Solving for the measured value and adding the DUT results in

This makes clear that the ground loop comprises two parts, the cable and the pin. Each contributes a resistance to the ground loop error.  

A common error is to use calibration to remove the ground loop error.  The calibration will subtract the constant value of R_measured from the result, which theoretically provides the correct measurement.

This method doesn’t work because the value of K is a constant, but the value of the cable and pin resistance is not.  Bending the cable or adding compression to the pin will change the value of the ground resistance by a small amount.  The ground resistance of BNC connectors, used on many VNA’s, is also not constant.  However, this small change in value is of the same order of magnitude as the DUT, while the cable and pin resistance is many orders of magnitude larger than the DUT.

This method attempts to take the difference between two very large numbers to obtain a very small result. This is often unsuccessful.

Introducing a Ground Isolator

The introduction of a ground isolator changes the equation to

In this case, the ground resistance is first divided by CMRR of the isolator, significantly reducing the sensitivity to small changes in the ground loop resistance.

A transformer isolator limits this CMRR at low frequency, while solid-state isolators do not. On the other hand, transformers typically work to a higher frequency than a solid-state isolator, so this is a tradeoff.  But the question is how much isolation is required for a reasonable measurement.

Assuming a willingness to tolerate a 10% ground loop error in our 40 uΩ measurement, the error term has to be less than 40 µΩ.

This allows us to solve for the required isolator CMRR to perform this measurement. 

The shield resistance of a 1-meter PDN cable is approximately 15 mΩ.  The resistance of the Picotest P2104A pin is also typically about 15mΩ, though contact pressure can vary quite a bit, and there is a significant tolerance.

The minimum CMRR to make the measurement is 77.5 dB at low frequency.

Reducing the Ground Loop Error With CMRR

To demonstrate the CMRR measurement requirements, an ideal, parameterized, Op Amp is inserted into the simulation setup shown in Figure 1 and is depicted in Figure 3. The results for a 2-port shunt measurement with 1-meter PDN cables and an ideal op amp is shown in Figure 4. The ideal op amp represents the ground loop isolator. The CMRR for an op amp with 57 dB and 77.5 dB is shown versus a result with no CMRR. The result with 57 dB of CMRR demonstrates another Picotest product, the J2113A. 

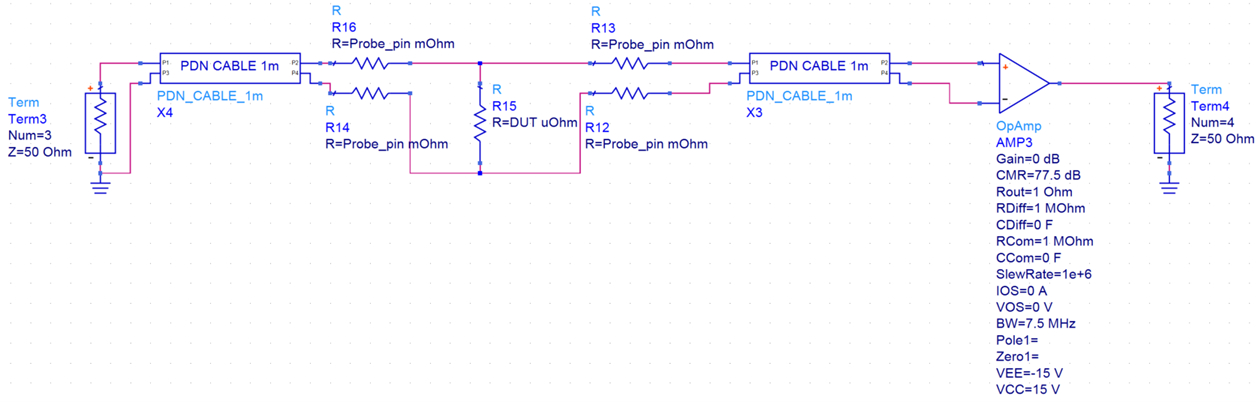Figure 4. 40 µΩ impedance measurement setup with 1-meter PDN cables and ideal op amp.

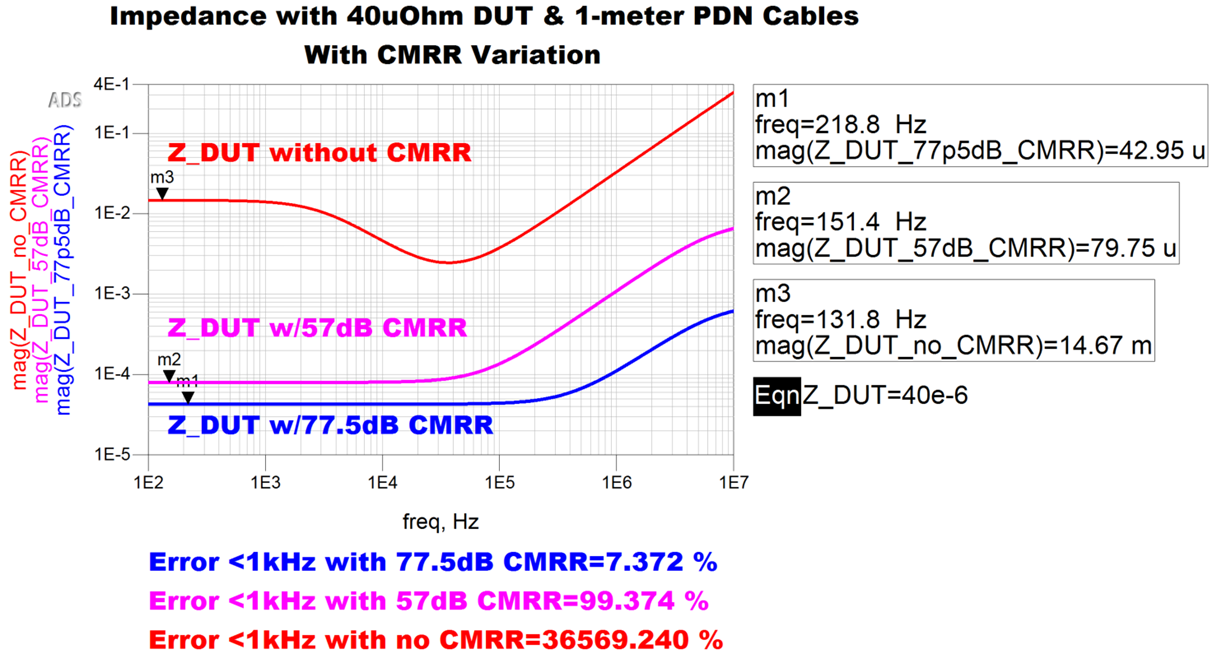Figure 5. 40 uΩ DUT impedance measurement setup with 1-meter PDN cables with CMRR variation.

As shown by Figure 4, an uncalibrated error of 7.4% for our 40 µΩ DUT is achieved when CMRR equals 77.5 dB. However, as shown in Figure 4, when CMRR is equal to 57 dB, the uncalibrated error is almost 100%. This again emphasizes the earlier point that measuring a 2000 Amp PDN at 40 µΩ is not easy or intuitive. Calibration can then be used to further improve this accuracy. 

Stay tuned for part two of this blog discussion, where it will be demonstrated how to measure a 40 uΩ DUT using a 2-port probe.

REFERENCES

1. Computing Processors, Ampere.
2. S. M. Sandler, “How to Measure Ultra-Low Impedance (100 uOhm and Lower) PDNs,” EDI CON, October 17, 2018.
3. A. K. Davis, S. M. Sandler, “The 2-Port Shunt-Thru Measurement and the Inherent Ground Loop,” EDI CON, October 2018.
4. P2102A 2-port Probe, Picotest.
5. P2104A , Picotest.
6. PDN Cable, Picotest.
7. J2113A Semi-Floating Differential Amplifier, Picotest.