Forward error correction (FEC) codes are necessary for modern high-speed links to achieve acceptably low bit error rates (BERs). The post-FEC BER of a link cannot be accurately estimated from only knowing the pre-FEC BER and the FEC architecture; other factors such as equalization techniques, decision feedback equalizer (DFE) error propagation, and the statistics of inter-symbol interference, crosstalk, and jitter must be considered. Ideally, one may perform a time-domain simulation to capture the characteristics of all error sources. However, simulations demonstrating the targeted <10-15 BERs are prohibitively long, especially for exploring architectural design alternatives. Therefore, an efficient statistical model that accurately predicts very low post FEC BERs serves an essential function in the design of high-speed wireline links.
Doubling the data-rate from the current 112 Gb/s per-lane systems to 224 Gb/s degrades signal integrity, resulting in less operating margin and a worse pre-FEC BER. Despite the progress being made on improving channel materials, transceiver architecture designs, and system level innovations, stronger FECs are needed to loosen pre-FEC BER requirements for 200+ Gb/s applications. To address this, the IEEE 802.3dj task force is considering a concatenated FEC architecture. It includes a strong, non binary linear block code as the outer FEC to correct burst errors. A simpler binary code is used as an inner code to provide another layer of protection against random bit errors.
This paper presents a statistical model to calculate the post-FEC BER of multi-part links with a concatenated FEC. The model offers a considerable advantage in computational efficiency over commonly used time-domain simulations. While time-domain simulations may take days to observe BERs at 10-8 levels and must be unreliably extrapolated to down to lower levels, our model accurately computes arbitrarily low BERs in only seconds.
Statistical Modeling Methodology
A Markov model can be used to describe the correlated errors introduced by a DFE-based receiver. By time-unrolling this Markov model, we build a trellis representing an outer-FEC codeword to analyze the probability of different possible error patterns. To limit the computational complexity of our analysis, we use four levels or hierarchy when building the trellis model of an outer-FEC codeword, shown in Figure 1. We track the number of bit errors and FEC symbol errors in each trellis path. To model the inner-FEC decoding process, we perform an inner-FEC correction step, eliminating bit errors in correctable trellis paths. At the end of the trellis path analysis, we calculate the post-FEC BER by finding the probability of trellis paths that are not correctable by the outer-FEC decoder. For example, using the industry standard RS-KP4 outer FEC code, trellis paths having more than 15 FEC symbol errors are not correctable.
Figure 1. Trellis model of a hypothetical concatenated FEC with a non-binary (2,1,1) outer code in GF(24) and a binary (10,8,1) inner code. This paper also includes a methodology for modelling inner-FEC miscorrections and inner-FEC codeword interleaving, factors that significantly impact link performance. Figure 2 shows an example of our simulation results for pre-FEC vs. post-FEC BER in links with a concatenated FEC. Links with and without a DFE are included, and the results are shown with and without inner FEC miscorrections.
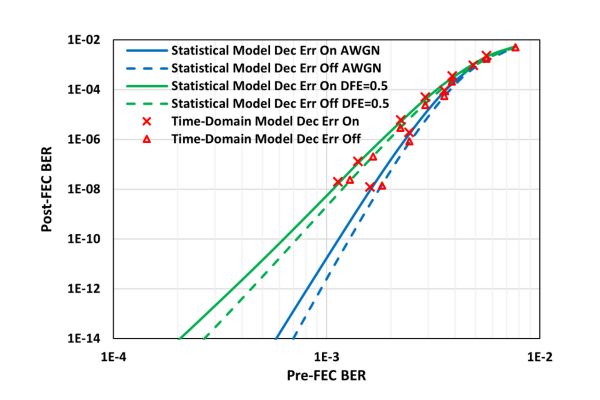Figure 2. Simulation Results for a RS-KP4 + Hamming (128,120) concatenated FEC.
Conclusion
The proposed model can serve as a tool for evaluating FEC choices in 200+ Gb/s applications. It allows us to compare the effect of different inner/outer codes and inner-FEC interleaving schemes on post-FEC BER. It can also be used as a tool for system-level transceiver design, allowing designers to see the impact of design choices on the post-FEC BER efficiently.
The paper referenced here received the Best Paper Award at DesignCon 2023. To read the entire DesignCon 2023 paper, download the PDF.
