…it depends
Which is better, tight coupled or loosely coupled differential pairs? How many decoupling capacitors should I use per power pin? Is 1 MHz enough bandwidth in my SSCG or do I need 3 MHz? Should I pay extra for ultra-thin dielectric in the power and ground planes? Will my channel still work if the channel impedance is 110 Ohms and not 100 Ohms?
Every designer faces these sort of questions on a daily basis. And, unfortunately, the most common answer to these questions and ALL engineering questions (and most others) is “…it depends.”
Every design has its own unique set of constraints, assumptions and tradeoffs. The right answer for one design may not be the right answer for another or even the next design. My co-author and good friend, Power Integrity expert, Larry Smith, says about power distribution networks, “Every PDN has its own story.”
The only way to answer “…it depends” questions is by analyzing the problem, including all the assumptions and dependencies, and then putting in the numbers with rules of thumb, analytical approximations or numerical simulations. Even with the numbers, how we use them will be different in different systems.
Every product has its own tradeoffs between the final performance and the three constraints of cost, schedule and risk. My friend and colleague, EMC expert, Bruce Archembault, often says, “Engineering is Geek for tradeoff analysis.”
This is one reason why engineering is hard.
Dispersion in Microstrips
Sometimes, putting in the numbers helps to identify a design constraint that may be irrelevant and a distraction to the real problems. For example, ask a microwave engineer about the problems using microstrip transmission lines and within the first sentence you will hear about the problem of dispersion. This is a frequency dependent speed of the signal. It also causes the characteristic impedance to be frequency dependent.
Dispersion can be a bad thing for high speed digital signals. It can smear out the edges, contributing to collapse of the eye. It is mentioned as an issue in most popular descriptions of microstrip transmission lines.
Does dispersion in microstrips cause a problem and should I avoid microstrips for my channel interconnects? The answer, of course, is, “…it depends.”
Analyzing Dispersion in Microstrips
This problem has been analyzed both analytically and numerical over the past 40 years. One of the best, early reviews of the analysis was presented by Martin Schneider, of Bell Labs, who did a lot of work on analytical approximations of other microstrip properties. In January, 1972, he published a short piece in the Proceedings of the IEEE, “Microstrip Dispersion.”
In this paper, he introduced an analytical approximation for the dispersion in microstrips. He normalized the speed of a signal, compared to the speed of light, c,

Dk0 is the bulk dielectric constant of the substrate at low frequency, assumed to be constant with frequency.
Dkeff is the effective, quasi-static dielectric constant of the microstrip given the combination of some field lines in air and some in the substrate.
fc is the cut off frequency of the TE1 surface wave, where dispersion begins to play a role.
The microstrip has a line width of w and a dielectric thickness of h
vnormalized is the relative phase velocity to the speed of light.
The useful feature of analytical approximations is that they can be put in a spreadsheet or simple analysis tool. The downside is, even though it may look very complicated, this is no indication of its accuracy. We need to compare it to either a numerical simulation or a measurement.
Schneider offered a comparison of his analytical approximation to measurements of the day. Reproduced in Figure 1 is his comparison.
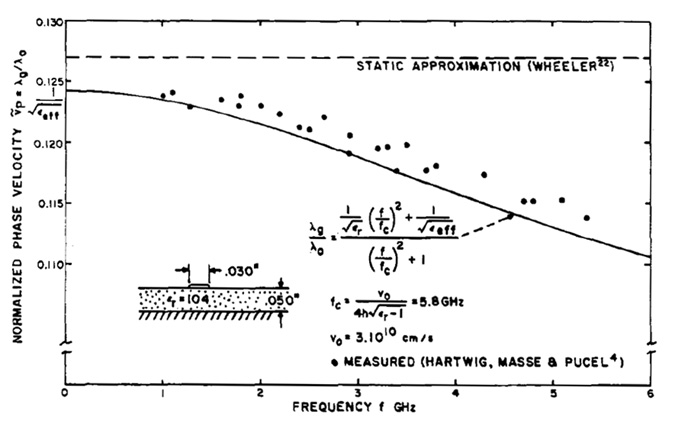
Figure 1. Taken from Schneider comparing his approximation to measurements.
Should you worry about dispersion in microstrips?
Your first reaction probably is, “wow! There is a lot of dispersion in microstrips, and look, it happens starting at 1 GHz. I better start worrying about microstrip dispersion.” This is the problem with generalizing one specific set of conditions to all conditions.
In Schneider’s day, microstrips were used for microwave applications with thick substrates and high dielectric constant substrates. These measurements corresponded to values of
Dk0 = 104
w = 30 mils
h = 50 mils
In this geometry, dispersion is pretty significant. But these conditions aren’t close to the typical geometries used in high speed digital applications, for example.
I had one of my CU, Boulder, graduate students, Gaurav Narula, who is now working at Cadence, implement these approximations in my favorite free, open source simulator tool, QUCS. The project file with the simulation and plots is available for download here.
We used more typical values for microstrip applications in high speed digital applications, with
Dk0 = 4
w = 5 mils
h = 3 mils
The dispersion is hardly noticeable even up to 100 GHz. Figure 2 shows the normalized velocity in microstrip for this condition, compared to the case Schneider analyzed, on the same scale.
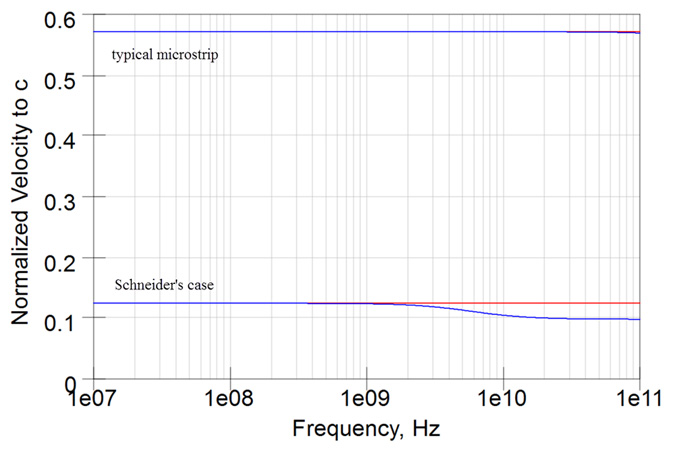
Figure 2. Dispersion in typical microstrip structures
A valuable figure of merit for the onset of the dispersion effects is the cutoff frequency. In the example Schneider compared to measurements, the cut off frequency was 5.8 GHz. In the case of the typical microstrip, the cut off frequency was 560 GHz.
Now that you are armed with a simple estimate for the dispersion in microstrips, you can put in the numbers for your application and decide for yourself.
Do microstrips show dispersion? Yes, absolutely. Should I worry about dispersion in the microstrips I use in my digital applications? Probably not. There are far more important and serious problems with microstrips that can pose real performance problems. But that’s another story…

