When I first started studying Maxwell’s Equations, I was always intrigued by its mathematical finesse. How could someone think of that? Today we take them for granted and we sometimes forget how amazing they are and what a genius the guy was. In my view, James Maxwell should be with, if not above, Einstein and Newton among the greatest physicists to ever live, but outside our field people seldom know who Maxwell was. That is a great injustice! So in today’s post, I will try to tell the tale of his equations, not from a mathematical point of view, which can be daunting to some people, but from a historical perspective. Maybe that way people can appreciate everything that went on 150 years ago.

We start our tale with some very scary equations. Ooh spooky! But don’t worry about them. We will see that they are not as bad as they look.

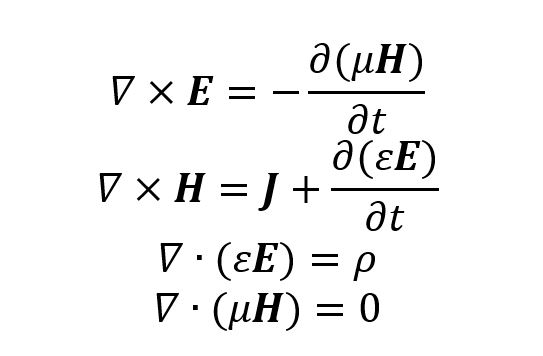
The last two are what we call Gauss Laws. The operator you see there simply means that if more lines of fields are entering a closed region than are exiting the same region, there must be some source for the lines inside that region. Think of it this way: if you were to enclose the entire Earth with a bubble, you would have more lines of the gravity field exiting the bubble than entering it. That would mean that there must be a source of the gravity field inside the bubble. In this case, we know the Earth is the source. For the electric field, we have

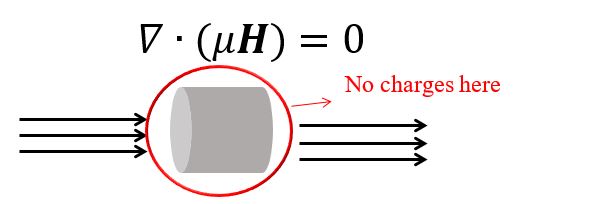
Since nobody has ever found a magnetic charge, we usually have the divergent of the magnetic field to be zero (if someone ever finds a magnetic charge, that will change).

Now that we are done with the appetizers we are ready for the main course! Until the beginning of the 19^th century, electricity and magnetism were fairly known, but thought to be completely independent phenomena. In 1820, Hans Oersted showed that there was a relationship between the two. And the funny part is that the discovery was done almost by accident: he was teaching a class on electric circuits and he noticed that his compass seemed to be influenced by the current. In 1827, Andre-Marie Ampere showed mathematically what that relationship was. It looked somewhat like the equation below, only a lot less elegant.  

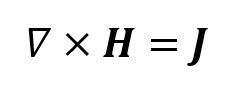
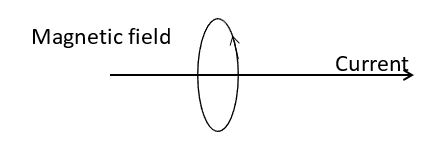
But what does the weird symbol before the H means? It is what we know as the curl operator, and it measures how much a field “loops around” without getting anywhere. Imagine a tornado that is not moving. We can say that there is no force outside the tornado, but the winds are curling around the eye of the storm with incredible power. And if we use a bubble around the tornado, we can say that its divergence is zero (no line of force is exiting the bubble). The gravity field has a nonzero divergent, but has zero curl. Our static tornado has zero divergent and nonzero curl. Any field (force, electric, etc.) can be decomposed in its divergent and curl components. So what Ampere’s Law tells us is that a current J creates a curl of magnetic field around it.

We are getting there. In 1831, Michael Faraday discovered electromagnetic induction. If he opened or closed the circuit shown below, he would observe current on the reader. Notice that it wouldn’t be the same as the Ampere’s Law: you would need a spike in the magnetic field to generate an electric field.

Faraday didn’t have a formal education, which was both a blessing and a curse. Because he didn’t learn what everyone else was learning (that only gravity can act at a distance), he could experiment and see what everyone else was missing. But at the same time, he was unable to put his ideas in a mathematical framework so the physicists of his time could understand it. He was left out of many discussions, and was perceived as a great experimentalist, but not as “part of the club.” He was growing old, sidelined by his peers, until a young man came about…

In 1860, Maxwell meets Faraday and sees what everyone else was missing. Not only was Faraday correct, but his idea made perfect mathematical sense: the “spike” in the magnetic field could be interpreted as a time-varying field (the ∂t term in the equation below).

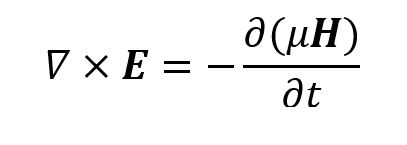
But Maxwell didn’t stop there. He revisited Ampere’s Law and saw that something was missing. In 1861 and 1862 he published a paper called On Physical Lines of Force, where he showed that electromagnetic propagation was not only possible, but was already happening: light! With some calculations, and the values for µ and ɛ from Gauss’ Laws, he determined the speed of light. But what did he do with it?

Take a look at the circuit below:

We all know I1 and I2 have the same value, but Maxwell showed that they cannot have the same nature. I1 is what we call conduction current, and is related to the electrons flowing through the wire. But the electrons cannot flow through the capacitor. Instead, they accumulate on either side of the capacitor, creating an electric field in it that changes with time. This change in field is what we call displacement current. It sounds simple now, but when Maxwell argued for it, there was no way of verifying it. This was one of the few times in science that the theory came before anyone could observe the related phenomenon.

Why is it important? Let’s forget conduction current J for a moment and focus only on the time-varying parts.

We saw from Faraday that if a magnetic field changes with time, it creates an electric field. Now Maxwell is saying that if an electric field changes with time, it creates a magnetic field. Can you see now that they are entangled? Magnetic creates electric and vice-versa, in a such a way that they now propagate! Even if you now remove conduction current J they continue to exist.

It was not until 1888 that Maxwell’s predictions could be confirmed. Heinrich Hertz was the first one to measure electromagnetic wave propagation. When asked about the use of it, Hertz replied “No use whatsoever. It is just an experiment to prove that Maxwell was right.” In 1901, Guglielmo Marconi performed the first transatlantic wireless communication. In 1905 Albert Einstein published the Theory of Relativity, using a lot of what Maxwell had shown. From there on, everything evolved so fast that we sometimes forget that the path to get there was not a straight one.

What if Oersted didn’t find, almost by accident, the connection between electric and magnetic fields? What if Faraday tried what everyone else was trying?  What if Faraday and Maxwell never met and exchanged ideas? What if Maxwell didn’t devote his time to this as he was always busy with something else (color photographs, statistical physics, Saturn rings, theory of heat, theory of gases)? I would say it is a safe bet that if Maxwell ever touched the subject, things would eventually be explained. But if he didn’t, we would probably be using messenger pigeons to this day. And maybe, just maybe, if he didn’t die in 1879 at the age of 48 and lived for another 20 years, we would have cities in Mars with intergalactic cars by now.